简介

贝叶斯定理是18世纪英国数学家托马斯·贝叶斯（Thomas Bayes）提出得重要概率论理论。以下摘一段 wikipedia 上的简介：

所谓的贝叶斯定理源于他生前为解决一个“逆概”问题写的一篇文章，而这篇文章是在他死后才由他的一位朋友发表出来的。在贝叶斯写这篇文章之前，人们已经能够计算“正向概率”，如“假设袋子里面有 N 个白球，M 个黑球，你伸手进去摸一把，摸出黑球的概率是多大”。而一个自然而然的问题是反过来：“如果我们事先并不知道袋子里面黑白球的比例，而是闭着眼睛摸出一个（或好几个）球，观察这些取出来的球的颜色之后，那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测”。这个问题，就是所谓的逆向概率问题。

贝叶斯定理的思想出现在18世纪，但真正大规模派上用途还得等到计算机的出现。因为这个定理需要大规模的数据计算推理才能凸显效果，它在很多计算机应用领域中都大有作为，如自然语言拼写检查，机器学习，推荐系统，图像识别，博弈论等等。

定义

贝叶斯定理是关于随机事件 A 和 B 的条件概率：

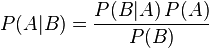
其中P(A|B)是在 B 发生的情况下 A 发生的可能性。

在贝叶斯定理中，每个名词都有约定俗成的名称：

P(A)是 A 的先验概率，之所以称为“先验”是因为它不考虑任何 B 方面的因素。
P(A|B)是已知 B 发生后 A 的条件概率，也由于得自 B 的取值而被称作 A 的后验概率。
P(B|A)是已知 A 发生后 B 的条件概率，也由于得自 A 的取值而被称作 B 的后验概率。
P(B)是 B 的先验概率，也作标淮化常量（normalizing constant）。

按这些术语，贝叶斯定理可表述为：

后验概率 = (相似度 * 先验概率)/标淮化常量

也就是说，后验概率与先验概率和相似度的乘积成正比。

另外，比例P(B|A)/P(B)也有时被称作标淮相似度（standardised likelihood），Bayes定理可表述为：

后验概率 = 标淮相似度 * 先验概率

条件概率就是事件 A 在另外一个事件 B 已经发生条件下的发生概率。条件概率表示为P(A|B)，读作“在 B 发生的条件下 A 发生的概率”。

联合概率表示两个事件共同发生（数学概念上的交集）的概率。A 与 B 的联合概率表示为。

推导

我们可以从条件概率的定义推导出贝叶斯定理。

根据条件概率的定义，在事件 B 发生的条件下事件 A 发生的概率为：

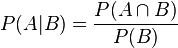
同样地，在事件 A 发生的条件下事件 B 发生的概率为：

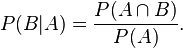
结合这两个方程式，我们可以得到：

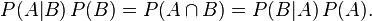
这个引理有时称作概率乘法规则。上式两边同除以 P(A)，若P(A)是非零的，我们可以得到贝叶斯定理:

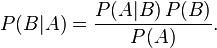
解释

通常，事件 A 在事件 B 发生的条件下的概率，与事件 B 在事件 A 发生的条件下的概率是不一样的；然而，这两者是有确定关系的，贝叶斯定理就是这种关系的陈述。

贝叶斯公式的用途在于通过己知三个概率来推测第四个概率。它的内容是：在 B 出现的前提下，A 出现的概率等于 A 出现的前提下 B 出现的概率乘以 A 出现的概率再除以 B 出现的概率。通过联系 A 与 B，计算从一个事件发生的情况下另一事件发生的概率，即从结果上溯到源头（也即逆向概率）。

通俗地讲就是当你不能确定某一个事件发生的概率时，你可以依靠与该事件本质属性相关的事件发生的概率去推测该事件发生的概率。用数学语言表达就是：支持某项属性的事件发生得愈多，则该事件发生的的可能性就愈大。这个推理过程有时候也叫贝叶斯推理。

示例

示例一：应当根据新情况更新先验概率

《决策与判断》第十二章中讲到人们都有保守主义情结，即使出现了新信息，也不愿意根据新信息来更新先验概率。用前面解释里面的话说就是：新信息是 B 事件不断发生，人们本应该根据这个信息去更新 A 事件发生的概率，但人们却更愿意固守之前估计的 A 事件发生的概率。

书中举了这样一个调查案例：

假设有两个各装了100个球的箱子，甲箱子中有70个红球，30个绿球，乙箱子中有30个红球，70个绿球。假设随机选择其中一个箱子，从中拿出一个球记下球色再放回原箱子，如此重复12次，记录得到8次红球，4次绿球。问题来了，你认为被选择的箱子是甲箱子的概率有多大？

调查结果显示，大部分人都低估了选择的是甲箱子的概率。根据贝叶斯定理，正确答案是96.7%。下面容我来详细分析解答。

刚开始选择甲乙两箱子的先验概率都是50%，因为是随机二选一（这是贝叶斯定理二选一的特殊形式）。即有：

P(甲) = 0.5， P(乙) = 1 - P(甲)；

这时在拿出一个球是红球的情况下，我们就应该根据这个信息来更新选择的是甲箱子的先验概率：

P(甲|红球1) = P(红球|甲) × P(甲) / (P(红球|甲) × P(甲) + (P(红球|乙) × P(乙)))
P(红球|甲)：甲箱子中拿到红球的概率
P(红球|乙)：乙箱子中拿到红球的概率

因此在出现一个红球的情况下，选择的是甲箱子的先验概率就可被修正为：

P(甲|红球1) = 0.7 × 0.5 / (0.7 × 0.5 + 0.3 × 0.5) = 0.7

即在出现一个红球之后，甲乙箱子被选中的先验概率就被修正为：

P(甲) = 0.7， P(乙) = 1 - P(甲) = 0.3；

如此重复，直到经历8次红球修正（概率增加），4此绿球修正（概率减少）之后，选择的是甲箱子的概率为：96.7%。

我写了一段 Python 代码来解这个问题：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

def bayesFunc(pIsBox1, pBox1, pBox2):
    return (pIsBox1 * pBox1)/((pIsBox1 * pBox1) + (1 - pIsBox1) * pBox2)

def redGreenBallProblem():
    pIsBox1 = 0.5

    # consider 8 red ball
    for i in range(1, 9):
        pIsBox1 = bayesFunc(pIsBox1, 0.7, 0.3)
        print " After red %d > in 甲 box: %f" % (i, pIsBox1)

    # consider 4 green ball
    for i in range(1, 5):
        pIsBox1 = bayesFunc(pIsBox1, 0.3, 0.7)
        print " After green %d > in 甲 box: %f" % (i, pIsBox1)

redGreenBallProblem()

在这个调查问题里面，8次红球与4次绿球出现的顺序并不重要，因为红球的出现总是使选择的是甲箱子的概率增加，而绿球的出现总是减少。因此，为了简化编程，我将红球出现的情况以及绿球出现的情况摆在一起了。

程序运行结果如下：

1
2
3
4
5
6
7
8
9
10
11
12

After red 1 > in 甲 box: 0.700000
After red 2 > in 甲 box: 0.844828
After red 3 > in 甲 box: 0.927027
After red 4 > in 甲 box: 0.967365
After red 5 > in 甲 box: 0.985748
After red 6 > in 甲 box: 0.993842
After red 7 > in 甲 box: 0.997351
After red 8 > in 甲 box: 0.998863
After green 1 > in 甲 box: 0.997351
After green 2 > in 甲 box: 0.993842
After green 3 > in 甲 box: 0.985748
After green 4 > in 甲 box: 0.967365

从程序运行结果来看，很明显可以看到红球的出现是增加选择甲箱子的概率，而绿球则相反。

示例二：频率更适合用来解答概率问题

《进化心理学》第十三章(428页)讲到人类的心理从进化角度来看，更偏好使用频率（我最近十次打猎八次有收获）而不是概率（我最近打猎有80%的成功率）。

书中举了同一个问题用不同方式表述使得问题的难易程度迥然不同：

表述一：有一种疾病的发病率是千分之一，医院有一种化验技术可以对这种疾病进行诊断，但是却有百分之五的误诊率（也即是说尽管有百分之五的人没有病，但是化验结果却显示为阳性(即假阳性)）。现在假设一个人的化验结果显示为有病，仅根据这一化验结果推测，那么这个人确实患病的概率有多大？

这个问题也可以用贝叶斯定理来解决，不过在看分析之前，你可以先估算下你自己的答案，然后再和正确答案比较。

这个问题的分析过程如下：

已知先验概率：P(患病) = 0.001，P(正常) = 0.999；
该化验技术的确诊率（即患病化验结果显示为阳性的概率）为：P(确诊率) = 1.00；
该化验技术的误诊率（即正常化验结果显示为阳性的概率）为：P(误诊率) = 0.05。

根据上面的数据，我们就能够推测出一个人化验为阳性的情况下，这个人确实患病的概率有多大：

P(患病|阳性) = P(患病) × P(确诊率) / (P(患病) × P(确诊率) + P(正常) × P(误诊率))
= 0.001 × 1.00 / (0.001 × 1.00 + 0.999 × 0.05)
= 0.0198
= 2%

结果让你大吃一惊吧，在没有其他症状增加患病概率的情况下，单凭化验结果显示为阳性来推测的话，其真实患病的概率还不到百分之二。

用频率作为信息来记忆或回忆更生动也更容易被提取，想想第一次打猎什么情形，第二次打猎什么情形，历历在目。正因为频率作为信息存储载体保留了事件的形象性，提高了记忆的可得性，因此在进化过程中人类的心理机制优先选择了频率而不是抽象的概率。而且在人类十多万年的进化过程中，出现概率概念的文明进程不过几千年，大脑还没有对进化到更适应抽象的概率的地步。

所以这个问题如果换成用频率来表述的话，相信你的答案会大大接近于正确答案。

表述二：在一千个人中，就有一个人患有X疾病（即发病率为千分之一），有一种化验技术，可以检验是否患有该疾病。如果一个人确实患有该病，化验结果可定显示为阳性。但有时候也会出现误诊，即在一千个完全健康的人中，有五十个人的化验结果显示为阳性（也即是说误诊率为百分之五）。

换成以频率方式来表述这个问题，答案就显然易见了：

P(患病|阳性) = 1/(1 + 50) = 1/51 = 0.0196 = 2%

通过这个例子，我们可以懂得，若能把概率问题转换成频率来表述，即便是需要使用贝叶斯这样复杂定理来计算的问题，也能轻而易举地解答。这就是《你的灯亮着么？》里面提到的“重述问题”的技巧。

示例三：在博弈论里面的应用

挑战者 B 不知道原垄断者 A 是属于高阻挠成本（为阻止 B 进入而花费的成本）类型还是低阻挠成本类型，但B知道，如果 A 属于高阻挠成本类型，B 进入市场时A进行阻挠的概率是20%（阻扰成本高，因此阻挠概率低）；如果 A 属于低阻挠成本类型，B 进入市场时 A 进行阻挠的概率是100%。

博弈开始时，B 认为 A 属于高阻挠成本企业的概率为70%，因此，B 估计自己在进入市场时，受到 A 阻挠的概率为：

P(阻挠) = 0.7 × 0.2 + 0.3 × 1.0 = 0.44

0.44 是在 B 给定 A 所属类型的先验概率下，A 可能采取阻挠行为的概率。

当 B 进入市场时，若 A 确实进行阻挠。根据贝叶斯定理，从 A 进行阻挠这一行为，B 可修正 A 属于高阻挠成本企业的概率为：：

P(高成本阻扰企业) = 0.7 × 0.2 ÷ 0.44 × 1.0 = 0.32

根据这一新的先验概率，B 估计自己在进入市场时，受到 A 阻挠的概率为：

P(阻挠) = 0.32 × 0.2 + 0.68 × 1 = 0.744

若 B 再一次进入市场时，A 又进行了阻挠。根据贝叶斯定理，从 A 再次进行阻挠这一行为，B 可修正 A 属于高阻挠成本企业的概率为

P(高成本阻扰企业) = 0.32 × 0.2 ÷ 0.744 × 1.0 = 0.086

这样，根据 A 一次又一次的阻挠行为，B 不断修正判断 A 为高阻挠成本的概率（越来越低了），从而越来越倾向于将 A 判断为低阻挠成本企业。

示例四：在计算机领域中的应用

贝叶斯定理在计算机领域中的应用那可是太多了，无论是在机器学习，自然语言处理，图像识别，推荐算法，搜索算法还是垃圾邮件处理中都大有用途。这些应用中都有一个特点，那就是根据既有输入，在庞大的已有数据库中寻找匹配程度（也即是发生概率）最高的那些项。由于这些话题太大，在这里就不展开了。

徐宥翻译过 Peter Norvig 写的一篇怎样写一个拼写检查器的文章，作者只用了 20 行 Python 代码就实现了拼写检查/纠错，相当强大。文章也写得深入浅出，推荐看看，翻译版本在这里。

参考

• WikiPedia 贝叶斯定理
• Mbalib 贝叶斯法则
• 《决策与判断》
• 《进化心理学》
• 刘未鹏数学之美番外篇：平凡而又神奇的贝叶斯方法
• Peter Norvig，徐宥译怎样写一个拼写检查器